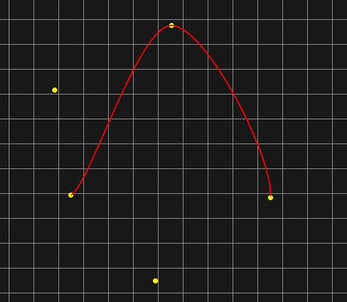
Catmull-Rom сплайни

1. Въведение

Catmull-Rom сплайновете са интерполационни криви, които преминават през даден набор от точки. Те се използват широко за изглаждане на траектории в графични приложения.

Даден е набор от точки P0, P1, P2, ... , Pn, където n >= 4, и целта е да се конструира плавна крива, която минава през тях.

2. Алгоритъм за построяване на Catmull-Rom сплайн

Точките се разделят на групи от по четири последователни точки:
P(i-1), P(i), P(i+1), P(i+2).
Кривата трябва да минава през P(i) и P(i+1), като осигурява плавни преходи между сегментите.

Изчисляване на тангентните вектори

За да определим формата на кривата, изчисляваме тангентните вектори в точките P(i) и P(i+1):

• T1 = (P(i+1) - P(i-1)) / 2
• T2 = (P(i+2) - P(i)) / 2

Тези вектори представляват приближена първа производна на кривата в съответните точки.

Построяване на гладък сегмент чрез алгоритъма на de Casteljau

Прилагаме алгоритъма на de Casteljau, за да построим кубичен Безиеров сегмент с контролни точки:

• B0 = P(i)
• B1 = P(i) + T1 / 3
• B2 = P(i+1) - T2 / 3
• B3 = P(i+1)

Стъпка 1: Първа итерация

• B0(1) = (1 - t) * B0 + t * B1
• B1(1) = (1 - t) * B1 + t * B2
• B2(1) = (1 - t) * B2 + t * B3

Стъпка 2: Втора итерация

• B0(2) = (1 - t) * B0(1) + t * B1(1)
• B1(2) = (1 - t) * B1(1) + t * B2(1)

Стъпка 3: Последна итерация

• B0(3) = (1 - t) * B0(2) + t * B1(2)

Намерената точка B0(3) лежи върху търсената крива.

3. Генериране на кривата

Чрез промяна на параметъра t в диапазона [0,1], се генерира един сегмент от сплайна. Процесът се повтаря за следващия сегмент, използвайки следващите четири точки, докато всички точки бъдат обработени.

Този метод гарантира гладка и непрекъсната интерполация, което го прави идеален за анимации, генериране на траектории и разработка на игри.